POTENCIACION
La potenciación es una operación matemática entre dos términos denominados: base a y exponente n. Se escribe a^n y se lee usualmente como «a elevado a n» o «a elevado a la n» y el sufijo en femenino correspondiente al exponente n. Hay algunos números especiales, como el 2, al cuadrado o el 3, que le corresponde al cubo. Nótese que en el caso de la potenciación la base y el exponente pueden pertenecer a conjuntos diferentes, en un anillo totalmente general la base será un elemento del anillo pero el exponente será un número natural que no tiene porqué pertenecer al anillo. En un cuerpo el exponente puede ser un número entero o cero.
RADICACION
En matemática, la radicación de orden n de un número a es cualquier número b tal que , donde n se llama índice u orden, a se denomina radicando, y b es una raíz enésima, por lo que se suele conocer también con ese nombre.



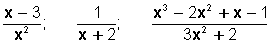
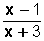 se multiplica por x + 2 en su numerador y denominador resulta:
se multiplica por x + 2 en su numerador y denominador resulta: