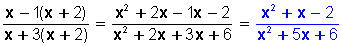DOMINIO Y RANGO DE UNA FUNCIÓN:
DOMINIO:
Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio, generalmente cuando se habla del plano, el dominio es el intervalo de valores que están sobre el eje de las X´s y que nos generan una asociación en el eje de las Y´s
RANGO O CODOMINIO
El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función o valores en el eje de las Y´s.



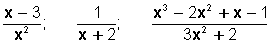
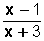 se multiplica por x + 2 en su numerador y denominador resulta:
se multiplica por x + 2 en su numerador y denominador resulta: